گردش وضعی و انتقالی سیارات

به‌نام خدا

در این مقاله، به مدت زمان، سرعت و دلیل این دو گردش در سیارات می‌پردازیم.

بخش اول: گردش وضعی

برای بررسی دلیل این نوع گردش سیارات، باید به ۴،۶۰۰،۰۰۰،۰۰۰ سال پیش سفر کنیم. زمانی که سیاره‌ها به این شکلی که می‌بینیم، وجود نداشتند.

در آن زمان ذرات گرد و غبار که دور تا دور خورشید را احاطه کرده و به دور آن در حال گردش بودند؛ بخاطر چسبیدن به هم و به وجود آوردن سیارات، نیروی چرخشی جدیدی تولید کردند که این امر باعث گردش وضعی سیاره‌ها شد. چون سیارات اگر حتی قطر چندین هزار کیلومتر داشته باشند، از ذرات کوچک به وجود آمده اند.

سرعت گردش وضعی در نقاط مختلف سیاره

در این مطلب، برای اندازه‌گیری سرعت گردش وضعی سیارات، سرعت خطی در استوای سیاره‌ها را محاسبه کرده‌ام. چون سرعت خطی نقاط سیاره در عرض‌های جغرافیایی مختلف متفاوت است؛ زیرا سرعت خطی در حرکت دایره‌ای  به فاصله مسیر حرکت تا محور مرکزی بستگی دارد؛ همان چیزی که شعاع دایره مسیر است.

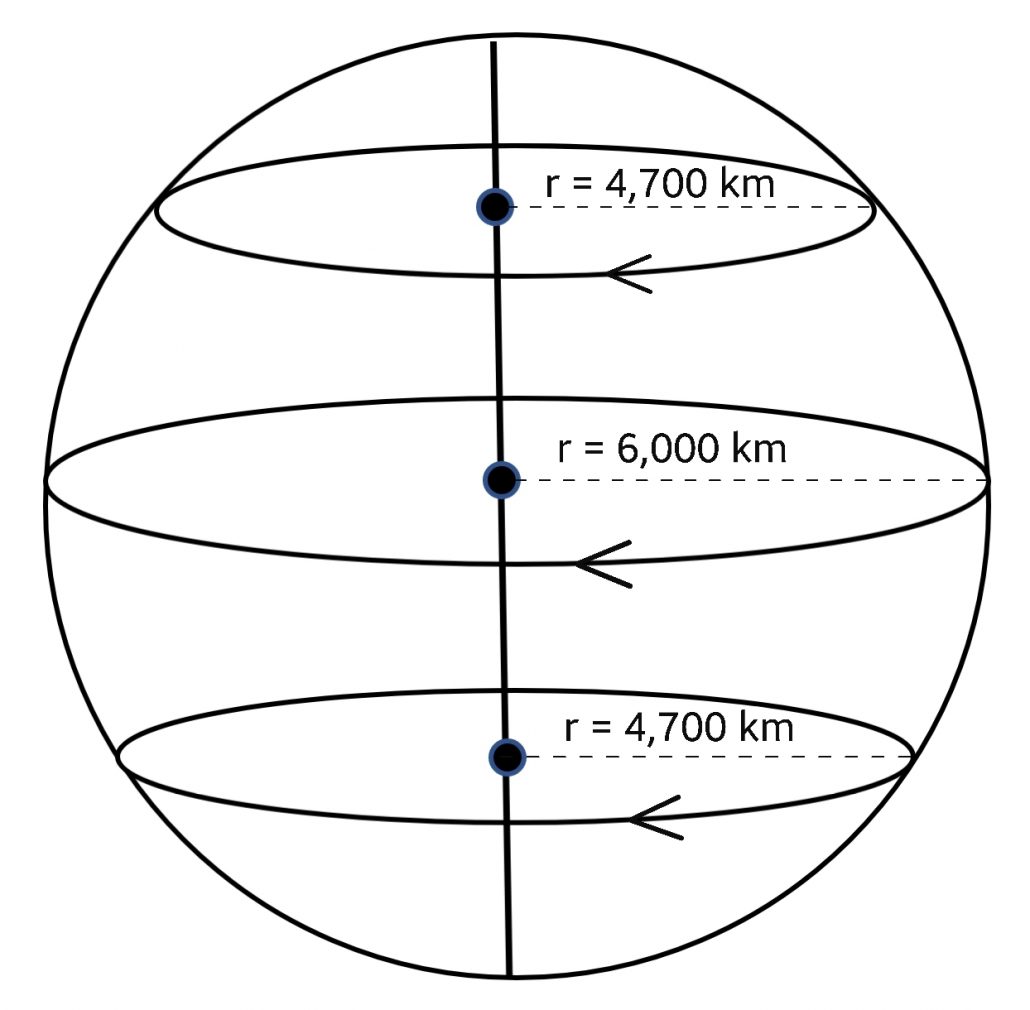
اکنون به مدت زمان و سرعت گردش وضعی سیارات می‌پردازیم.

عطارد

مدت زمان گردش این سیاره، به روز اندازه‌گیری می‌شود.

مدت زمان:   روز    ساعت    دقیقه    ثانیه

                  ۵۸      ۱۵         ۳۰       ۳۰

با توجه به این مدت زمان و اینکه قطر عطارد، ۴،۸۷۹ کیلومتر است، سرعت گردش وضعی آن ۳٫۰۳ متر در ثانیه است. یعنی هر نقطه در استوای عطارد، با سرعت ۳٫۰۳ متر در ثانیه حرکت می‌کند. برای تصور بهتر، در هر ثانیه، یک واحد مسکونی را طی می‌کند. اگر زمین این سرعت را داشت، طول روز‌ها به ۱۵۳ روز و ۱۰ ساعت می‌رسید.

روش به دست آوردن سرعت گردش وضعی در استوا: ابتدا قطر سیاره را ضربدر عدد پی یا ۳٫۱۴ می‌کنیم. اینگونه طول خط استوا آن به دست می‌آید. اگر دوره تناوب وضعی سیاره به روز است، طول خط استوا را تقسیم بر مدت گردش وضعی به روز می‌کنیم. اکنون سرعت به روز/کیلومتر (خوانده می‌شود: کیلومتر بر روز) به دست آمد. حالا برای تبدیل آن به ساعت، باید عدد به دست آمده را تقسیم بر ۲۳٫۹۳۴۵۲۵ ساعت کنیم.

به احتمال زیاد تا به حال با این عدد رو به رو نشده‌اید. این عدد، مدت زمان دقیق گردش وضعی زمین است؛ که معادل ۲۳ ساعت و ۵۶ دقیقه و ۴ ثانیه و ۰٫۰۹ ثانیه می‌باشد. اکنون سرعت روز/کیلومتر را تبدیل به ساعت/کیلومتر (خوانده می‌شود: کیلومتر بر ساعت) کردیم، کار ساده می‌شود. عدد به دست آمده را دو بار تقسیم بر ۶۰ می‌کنیم که ابتدا تبدیل دقیقه/کیلومتر و سپس تبدیل به ثانیه/کیلومتر شود.

زهره

مدت زمان گردش وضعی این سیاره هم به روز اندازه‌گیری می‌شود.

مدت زمان[۱]:    روز    ساعت    دقیقه    ثانیه

                   ۲۴۳       ۰         ۱۴       ۲۴

در نتیجه، با استفاده از فرمول بخش قبل، سرعت گردش وضعی این سیاره در استوا، ۱٫۸۱ متر در ثانیه است. یعنی به اندازه قد یک انسان بالغ در ثانیه. اگر زمین این سرعت را داشت، طول یک شبانه روز، ۲۵۶ روز و ۱۹ ساعت و ۴۲ دقیقه می‌شد.

قطر زهره ۱۲،۱۰۴ کیلومتر است.

[۱] در جهت معکوس، به دلیل °۱۷۷ انحراف محوری

زمین

به مدت زمان گردش وضعی زمین، در قسمت «عطارد» اشاره شد.

مدت زمان:    ساعت    دقیقه    ثانیه

                     ۲۳         ۵۶      4.09

روش به دست آوردن سرعت گردش وضعی در استوا: از زمین به بعد، مدت زمان گردش وضعی سیارات به ساعت اندازه‌گیری می‌شود. پس این فرمول تا انتهای بخش گردش وضعی به کار می‌آید.

ابتدا قطر را ضربدر عدد پی کرده و سپس تقسیم بر عدد دقیق گردش وضعی زمین به ساعت، یعنی  ۲۳٫۹۳۴۵۲۵ می‌کنیم. اکنون دو بار تقسیم بر ۶۰ می‌کنیم که تبدیل به ثانیه/کیلومتر شود. در نتیجه سرعت گردش وضعی زمین در استوا، ۴۶۴٫۸۵ متر در ثانیه است؛ یا به اندازه ارتفاع برج میلاد در هر ثانیه.

قطر زمین، ۱۲،۷۵۶ کیلومتر است.

مریخ

مدت زمان گردش وضعی مریخ، بسیار شبیه به زمین است و تنها ۴۱ دقیقه و ۲۰ ثانیه تفاوت دارد.

مدت زمان:    ساعت    دقیقه    ثانیه

                 ۲۴        ۳۷       ۲۴

سرعت گردش وضعی مریخ، ۲۴۰ متر در ثانیه است، یعنی در هر ثانیه، ۱۰ ساختمان مسکونی ۵ طبقه را می‌پیماید. اگر زمین، این سرعت دوران وضعی را داشت، طول یک روز تغییر زیادی نمی‌کرد و تبدیل به ۱ روز و ۲۲ ساعت و ۲۵ دقیقه می‌شد.

قطر مریخ، ۶،۷۹۰ کیلومتر است.

مشتری

این سیاره که بزرگترین کره بعد از خورشید می‌باشد (در منظومه شمسی)، کوتاه‌ترین مدت گردش وضعی بین سیاره‌ها را دارد. «مدت زمان گردش وضعی مشتری در استوا، کمتر از مناطق بالاتر و پایین‌تر آن است. به طوری که در سیستم ||، مدت زمان گردش وضعی، ۹ ساعت و ۵۵ دقیقه و ۴۰٫۶۳۲ ثانیه است و عددی که در بخش «مدت زمان» نوشته شده، مربوط به استوا است.»

منبع مطالب با رنگ نارنجی: کتاب «زمین از فضا» نویسنده: مهندس احمد دالکی، از موسسه جغرافیایی و کارتوگرافی گیتاشناسی.
البته بخش جامد مشتری یعنی هسته، در زمانی میانگین بین این دو حرکت می‌کند. چون تمام بخش‌های یک کره جامد به یکدیگر متصل‌اند.

مدت زمان‌:    ساعت    دقیقه    ثانیه

                      ۹          ۵۵    30.003

سرعت حرکت وضعی این سیاره، ۱۲٫۶۵۶  کیلومتر در ثانیه است. یعنی در یک ثانیه، جزیره هرمز را طی می‌کند. این سرعت زیاد اگر متعلق به زمین بود، طول روز در ۵۳ دقیقه فشرده می‌شد.

قطر مشتری، ۱۴۲،۹۸۴ کیلومتر است.

زحل

این سیاره دومین سیاره بزرگ منظومه‌ شمسی است و همچنین بعد از مشتری، در کوتاه‌ترین مدت زمان به دور خود می‌گردد.

نکته: اجزا حلقه‌های زحل، یعنی سنگ و یخ، همزمان با گردش وضعی زحل، در مدار خود می‌گردند.

برای بیشتر دانستن درباره خانواده زحل، به مطلب «۱۰ دانستنی ضروری از سیاره زحل»، مراجعه کنید.

مدت زمان:    ساعت    دقیقه    ثانیه

                      ۱۰        ۳۹       ۲۴

سرعت گردش وضعی این سیاره، تفاوت چندانی با مشتری ندارد، هر چند که در مقایسه با سرعت چرخش وضعی سیارات درونی، زیاد است. زحل با سرعت ۹٫۸۶۶ کیلومتر در ثانیه به دور خود می‌گردد. برای درک بهتر، در ۰٫۹ ثانیه ارتفاع کوه اورست ( ۸٫۸۴۹  کیلومتر ) را طی می‌کند. اگر زمین این سرعت را داشت، طول روز‌ها تنها ۱ ساعت و ۸ دقیقه می‌شد!

قطر زحل، ۱۲۰،۵۳۶ کیلومتر است.

اورانوس

این سیاره به پهلو خوابیده، ۹۷٫۸ درجه انحراف محوری دارد. به همین دلیل در دو فصل این سیاره، گردش وضعی به وجود آورنده شب و روز نیست. بخاطر اینکه جهت حرکت وضعی آن با مدارش، ۹۷٫۸ درجه زاویه دارد.

مدت زمان:    ساعت    دقیقه    ثانیه

                     ۱۷         ۳۶        ۰

سرعت گردش وضعی این سیاره، ۲٫۵۳۳ کیلومتر در ثانیه است. یعنی در ۱ دقیقه، طول استان قم را می‌پیماید. اگر سرعت گردش وضعی زمین مانند اورانوس بود، تنها ۲ ساعت و ۱۲ دقیقه فرصت دیدن ستارگان را داشتید (طول یک روز به ۴ ساعت و ۲۳ دقیقه می‌رسید).

قطر اورانوس، ۵۱،۱۲۰ کیلومتر است.

نپتون

این سیاره که چهارمین سیاره بزرگ و سومین سیاره پرجرم منظومه شمسی است، در مدت زمان کوتاه‌تری نسبت به اورانوس، یک بار به دور خود می‌چرخد.

مدت زمان:    ساعت    دقیقه    ثانیه

                     ۱۶          ۶        ۳۶

سرعت دوران وضعی این سیاره، ۲٫۷۷ کیلومتر در ثانیه می‌باشد، که با اورانوس تفاوت چندانی ندارد.

اگر زمین با این سرعت به دور خود می‌چرخید، به تنها ۴ ساعت زمان احتیاج داشت.

قطر نپتون، ۴۹،۵۳۰ کیلومتر است.

بخش دوم: گردش انتقالی

احتمالا از دلیل این نوع گردش سیارات باخبر هستید؛ جاذبه ستاره میزبان. ابتدا تصور می‌شد که زمین مرکز کیهان است و خورشید، ماه و سیارات منظومه شمسی دور آن می‌گردند. اما ثابت شد که خورشید، ۳۳۳،۲۲۱ بار از زمین پرجرم‌تر است. طبیعتا هم جرم سنگین‌تر نمی‌تواند دور جسم کم‌جرم‌تر بگردد. پس معلوم شد که سیارات، قمر‌ها، کوتوله‌ها، سیارک‌ها و دنباله‌دار‌ها، در مدارهای مشخصی گرد خورشید می‌گردند.

۲-۱ قوانین مداری کپلر

قوانین کپلر، توسط ستاره‌شناس آلمانی، یوهانس کپلر[۱] مطرح شده است و سه قانون را درباره حرکت سیارات در مدارشان مطرح می‌کند. او و تیکوبراهه[۲]، ستاره‌شناس دانمارکی در یک رصدخانه کار می‌کردند. بعد از مرگ تیکوبراهه، کپلر اطلاعات رصدی دقیق او را در اختیار داشت و بعد از ۲۰ سال محاسبه و تفکر، این سه قانون مداری سیارات را کشف و اعلام کرد.

[۱] Johannes Kepler (1571-1630)

[۲] Tycho Brahe (   (1546-1601

قانون اول:

این قانون می‌گوید: سیارات در مداری بیضوی به دور ستاره خود می‌گردند و ستاره در یکی از کانون‌های F1 یا F2 قرار دارد.

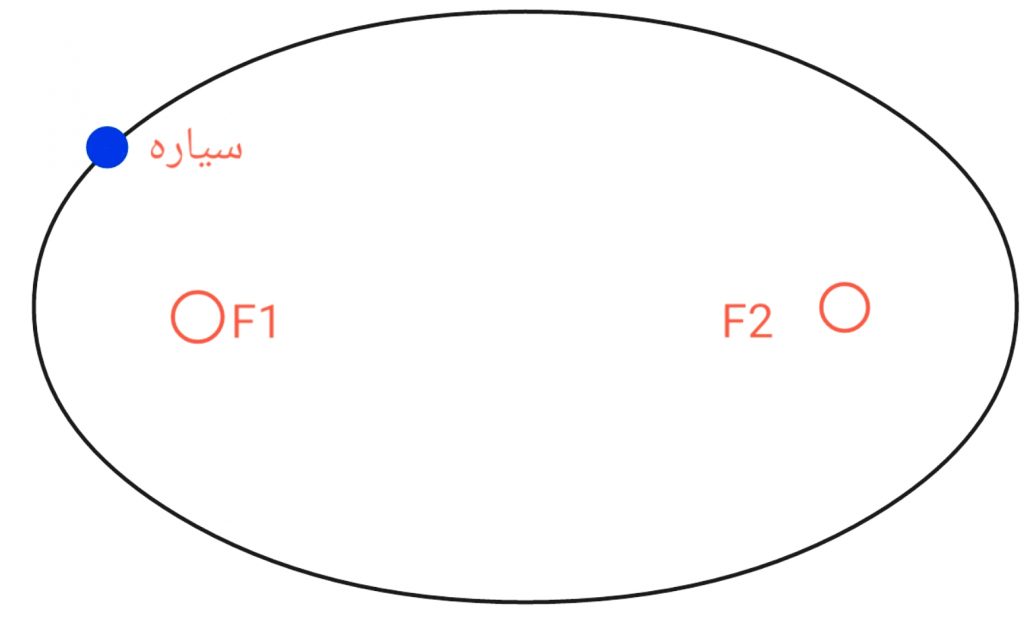
البته مدار همه سیارات، مانند تصویر بالا نیست؛ بلکه حتی ممکن است ۰٫۰۰۱ با دایره تفاوت داشته باشد، اما هیچ وقت دایره نیست. برای اندازه‌گیری این حد، از یک واحد سنجش به نام «خروج از مرکز مدار» استفاده می‌شود. علامت اختصاری آن، حرف e است.

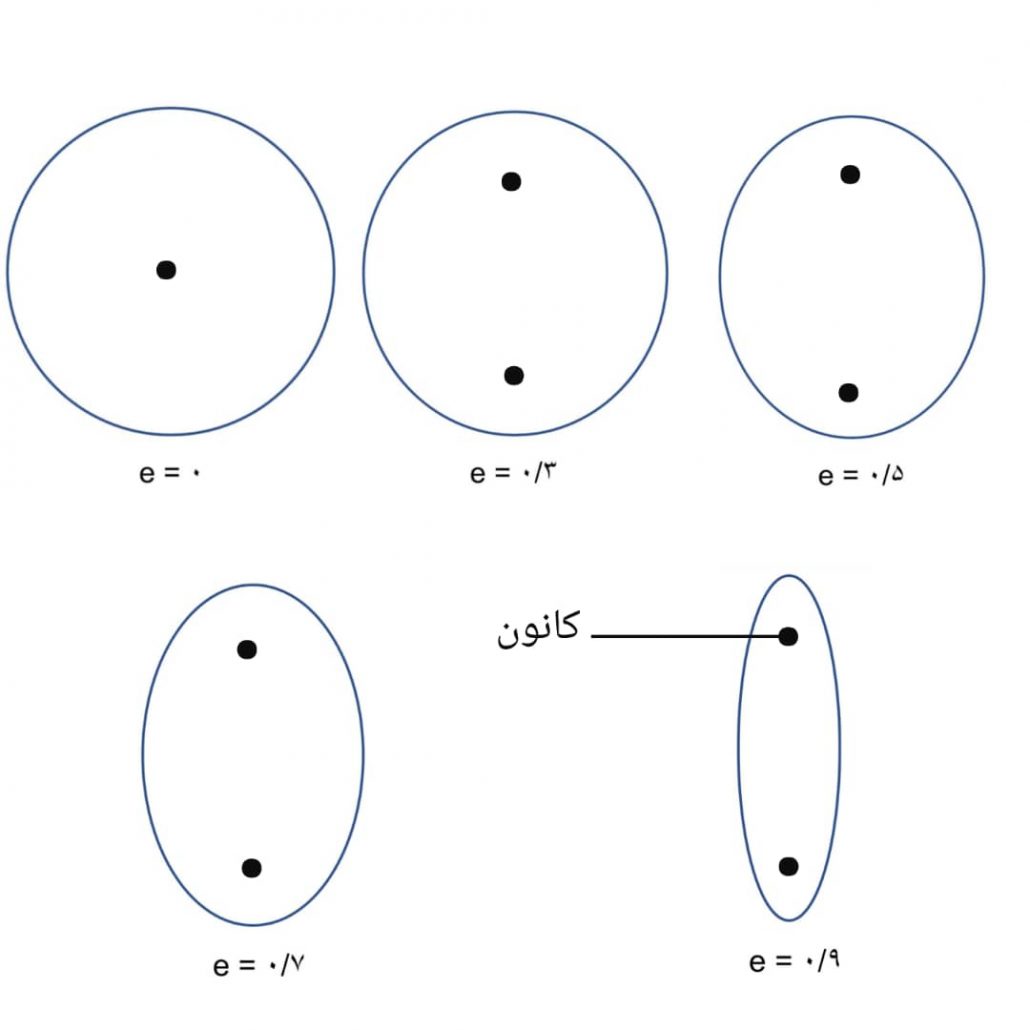
فرمول: e=c/a

روش انجام: در مدار سیاره، c را کانونی که ستاره در آن است در نظر می‌گیریم. یعنی c به معنی فاصله ستاره تا مرکز مدار است. a هم فاصله مرکز مدار تا لبه مدار است. اکنون ما باید c را تقسیم بر a کنیم.

قانون دوم:

هر چقدر که یک سیاره به ستاره خود نزدیک‌تر باشد، در مدار خود، مسافت کمتری را طی می‌کند. این قانون می‌گوید که وقتی یک سیاره به کمترین فاصله از ستاره خود می‌رسد، سرعت بیشتری پیدا می‌کند تا در زمان یکسانی، مسافتی یکسان را طی کند.

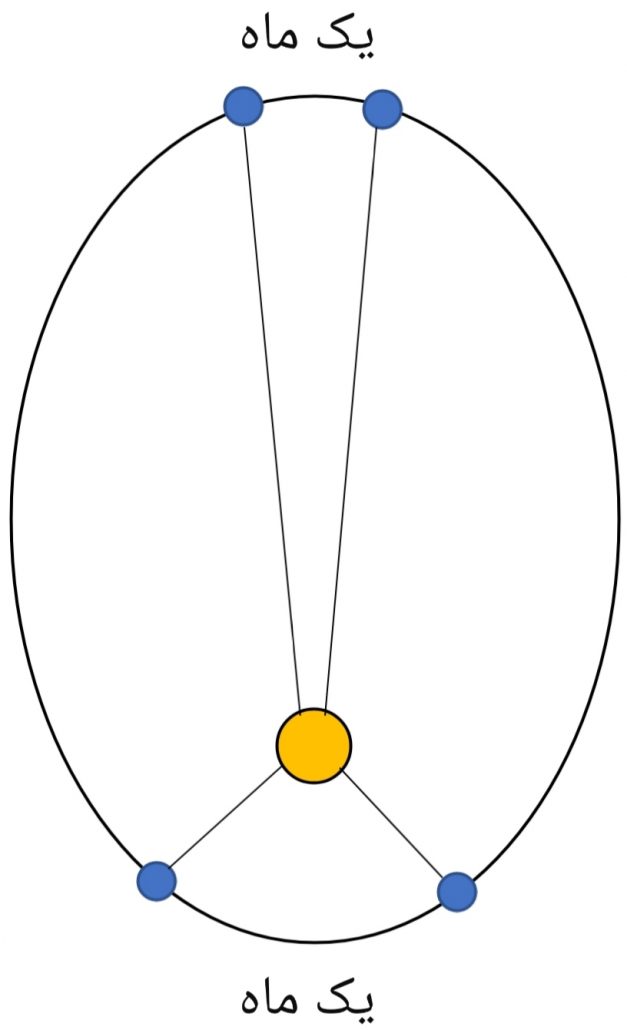
قانون سوم:

به سراغ آخرین قانون مداری کپلر می‌رویم که می‌گوید: مدت زمان یک دور گردش انتقالی، با فاصله سیاره تا ستاره خود متناسب است. به عبارت دیگر می‌توان گفت که مربع زمان تناوب چرخش سیارات به دور خورشید با مکعب نصف محور بزرگ بیضی متناسب است.

فرمول این قانون به این شکل می‌باشد:

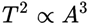
علامت T: به معنای دوره تناوب گردش سیاره به سال زمینی است.

علامت A: به معنای فاصله سیاره تا ستاره به واحد نجومی[۱] یا AU است. هر واحد نجومی ‌برابر فاصله میانگین زمین تا خورشید است که معادل ۱۴۹،۵۹۷،۸۸۷.۵ کیلومتر است. برای آوردن فاصله سیاره بهتر است از فاصله میانگین استفاده کنید (به دلیل خروج از مرکز مدار).

[۱] Astronomical unit

مثال: مشتری

فاصله میانگین تا خورشید: ۵٫۲۰۵ واحد نجومی‌   |    دوره تناوب انتقالی: ۱۱٫۸۶ سال

  ۱۴۰٫۶ = ۵٫۲³

۱۴۰٫۶۶ = ۱۱٫۸۶²

منابع قوانین کپلر: ویکی پدیا و دانشنامه رشد.

عطارد

این سیاره چون فاصله کمی نسبت به سیارات دیگر از خورشید دارد، جاذبه بیشتری روی آن اعمال می‌شود و به همین دلیل هر چقدر از مرکز منظومه شمسی دورتر می‌شویم، سرعت مداری کمتر شده و مدت زمان گردش انتقالی بیشتر.

مدت زمان:    روز    ساعت    دقیقه

                   ۸۷      ۲۳         ۱۳

همانطور که در بخش قوانین مداری کپلر دیدیم، مدار تمام سیارات بیضوی است و سرعت آنها در حضیض و اوج، متفاوت است. پس برای به دست آوردن سرعت مداری، از فاصله میانگین استفاده می‌کنم.

سرعت مداری عطارد، ۴۸٫۳۴ کیلومتر در ثانیه است. یعنی اگر زمین این سرعت را داشت، طول سال به ۲۲۵ روز و ۱۳٫۲۵ ساعت می‌رسید.

نحوه به دست آوردن: این روش برای این سیاره تا مریخ به کار می‌رود؛ اما برای مشتری تا نپتون که دوره تناوب انتقالی‌شان به سال اندازه‌گیری می‌شود، روش دیگر را معرفی می‌کنم.

ابتدا، فاصله قطر مدار سیاره را با ضرب در ۲ کردن فاصله سیاره تا خورشید به دست می‌آوریم سپس ضرب در عدد پی (۳٫۱۴) می‌کنیم تا محیط مدار به دست آید. سپس، تقسیم بر دوره تناوب انتقالی به روز می‌کنیم تا سرعت به روز/کیلومتر به دست آید. اکنون تقسیم بر عدد ۲۳٫۹۳۴۵۲۵، طول روز زمین به ساعت می‌کنیم تا به ساعت/کیلومتر به دست بیاوریم. حالا دو بار تقسیم بر ۶۰ می‌کنیم که ابتدا تبدیل به دقیقه/کیلومتر و بعد تبدیل به ثانیه/کیلومتر شود.

فاصله میانگین عطارد تا خورشید، ۵۸،۳۴۳،۱۷۶.۱۲۵ کیلومتر ( ۰٫۳۹ واحد نجومی‌) است.

زهره

یک سال این سیاره، از یک روز آن کوتاه‌تر است. در بخش گردش وضعی اشاره شد که یک روز زهره، ۲۴۳٫۰۱ روز است و در جهت معکوس می‌چرخد. اما مدت زمان سال آن به این میزان می‌باشد:

مدت زمان:    روز    ساعت    دقیقه

                  ۲۲۴      ۱۹      8.857

سرعت مداری این سیاره، ۳۵٫۱۶۴ کیلومتر در ثانیه است. اگر زمین با این سرعت در مدار خود می‌چرخید، در عرض ۳۱۰ روز و ۱٫۶۷ ساعت، سال خود را به اتمام می‌رساند.

فاصله میانگین زهره تا خورشید، ۱۰۸،۴۵۸،۴۶۸.۴۴ کیلومتر (۰٫۷۲۵ واحد نجومی‌) است.

زمین

قطعا تا به حال شنیده‌اید که یک سال زمینی ۳۶۵ روز است؛ اما در این بخش عدد دقیق‌تری را بیان   می‌کنم.

مدت زمان:    روز    ساعت    دقیقه

                  3۶۵       ۶        ۱۶/۸
 سرعت مداری سیاره‌مان، ۸۵۱/۲۹ کیلومتر در ثانیه است.

یک سال زمینی به روز را می‌توانیم به این گونه بنویسیم: ۳۶۵٫۲۵۶۳۶۶

فاصله میانگین زمین تا خورشید، ۱۴۹،۵۹۷،۸۸۷.۵ ۱۴۹۵۹۷۸۸۷٫۵ کیلومتر (۱ واحد نجومی‌) است.

مریخ

این سیاره بعد از زهره و عطارد، نزدیک‌ترین مدت گردش انتقالی را به زمین دارد و اگر در آن باشید، هر ۹/۱ سال زمینی، یک سالتان می‌شد. البته در بخش‌های بعد که به سیارات بیرونی می‌رسیم، باید مدت بیشتری برای تولدتان صبر کنید و یا شاید اصلا به تولد یک سالگی هم نرسید!

مدت زمان:    روز    ساعت    دقیقه

                  ۶۸۶      ۲۳      27.35

سرعت مداری مریخ، ۲۴٫۲ کیلومتر در ثانیه است. اگر زمین با این سرعت به دور خورشید می‌چرخید، یک سال به اندازه ۴۵۰ روز و ۱۳٫۱۲۲ ساعت طول می‌کشید.

فاصله میانگین مریخ تا خورشید، ۲۲۸،۱۳۶،۷۷۸.۴۴ کیلومتر ( ۱٫۵۲۵ واحد نجومی‌) است.

مشتری

اکنون، به منظومه شمسی بیرونی رسیدیم و یک سال در سیاره‌های باقی مانده، خیلی طول می‌کشد. همچنین در بخش‌های بعدی، روشی جدید را برای به دست آوردن سرعت مداری معرفی می‌کنم.

مدت زمان:    سال    ماه    روز

                    ۱۱     ۱۰   14.12

سرعت مداری مشتری، ۱۳٫۱ کیلومتر در ثانیه است. یعنی اگر زمین این سرعت را داشت، یک سال به اندازه ۸۳۲ روز و ۷٫۴۳۲ ساعت طول می‌کشید.

روش به دست آوردن سرعت مداری: این روش برای این سیاره تا نپتون که دوره تناوب انتقالی‌شان به سال اندازه‌گیری می‌شود، استفاده می‌شود. ابتدا فاصله میانگین سیاره تا ستاره را ضربدر ۲ و سپس ضربدر عدد پی (۳٫۱۴) می‌کنیم تا محیط مدار به دست آید. اکنون آن را تقسیم بر دوره تناوب به سال می‌کنیم و سرعت به سال/کیلومتر به دست آمد. حالا تقسیم بر روز‌های یک سال زمینی یعنی ۳۶۵٫۲۵۶۳۶۶ می‌کنیم تا سرعت به روز/کیلومتر برسد. سپس تقسیم بر یک روز زمینی به ساعت یعنی ۲۳٫۹۳۴۵۲۵ کرده و سرعت تبدیل به ساعت/کیلومتر شود. در مرحله آخر، دو بار تقسیم بر ۶۰ می‌کنیم تا تبدیل به ثانیه/کیلومتر شود.

فاصله میانگین مشتری تا خورشید، ۷۷۸،۶۵۷،۰۰۴.۴۴ کیلومتر ( ۵٫۲۰۵ واحد نجومی‌) است.

زحل

اکنون به بخشی از منظومه شمسی رسیده‌ایم که فاصله سیاره تا سیاره قبلی، به اندازه فاصله سیاره قبلی تا خورشید است.

مدت زمان:    سال    ماه    روز

                    ۲۹      ۵    18.02

سرعت مداری این سیاره، ۹٫۶۵ کیلومتر در ثانیه است. یعنی سرعت مداری این سیاره از سرعت گردش وضعی این سیاره که ۹٫۸۶۶ کیلومتر در ثانیه است، کمتر می‌باشد. اگر زمین چنین سرعتی در مدار خود داشت، یک سال به ۱،۱۲۸ روز و ۲۰٫۸۷۸۳ ساعت تبدیل می‌شد.

فاصله میانگین زحل تا خورشید، ۱،۴۲۴،۹۱۹،۸۷۸.۴۳ کیلومتر ( ۹٫۵۲۵ واحد نجومی‌) است.

اورانوس

حالا دیگر ده‌ها واحد نجومی با خورشید فاصله داریم. در اینجا، محیط مدار سیاره، از قطر منظومه شمسی هم بزرگ‌تر است.

مدت زمان:    سال    ماه    روز

                    ۸۴       ۴   11.49

سرعت مداری این سیاره یخبندان، ۶٫۷۹ کیلومتر در ثانیه است. به قدری کم است که اگر زمین با این سرعت مدار خود را طی می‌کرد، ۴٫۳۹۶ سال زمان لازم داشت.

فاصله میانگین اورانوس تا خورشید، ۲،۸۷۰،۷۸۳،۴۶۱٫۱۲ کیلومتر ( ۱۹٫۱۹ واحد نجومی‌) است.

نپتون

اکنون به آخرین سیاره منظومه شمسی رسیده‌ایم. اگر انسان در آن زندگی می‌کرد. تنها چند صدم یا هزارم درصد شانس داشت تا یک ساله شود. یعنی از زمانی که کشف شده، تنها ۰۶/۱ سال خود را گذرانده (این سیاره در سال ۱۸۴۶ کشف شد).

مدت زمان:    سال    ماه    روز

                   ۱۶۴     ۹    18.55

سرعت مداری نپتون، ۵٫۴۴۶ کیلومتر در ثانیه است. اگر زمین این سرعت را در مدار انتقالی خود داشت، ۵٫۴۸ سال زمان می‌برد تا یک دور گرد خورشید بچرخد.

میانگین فاصله نپتون تا خورشید، ۴،۴۹۷،۶۶۰،۴۸۷٫۶۷ کیلومتر (۳۰٫۰۶۵ واحد نجومی‌) است.

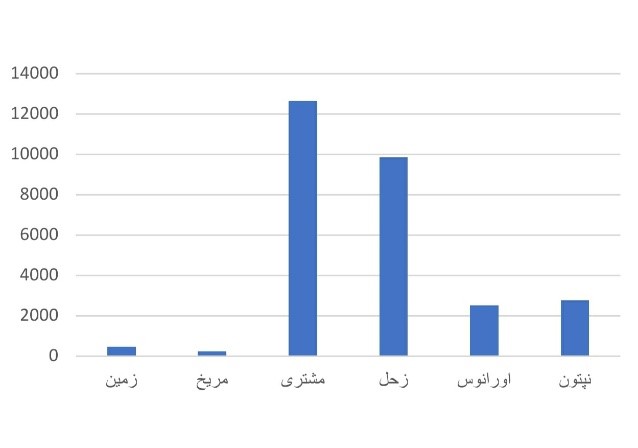
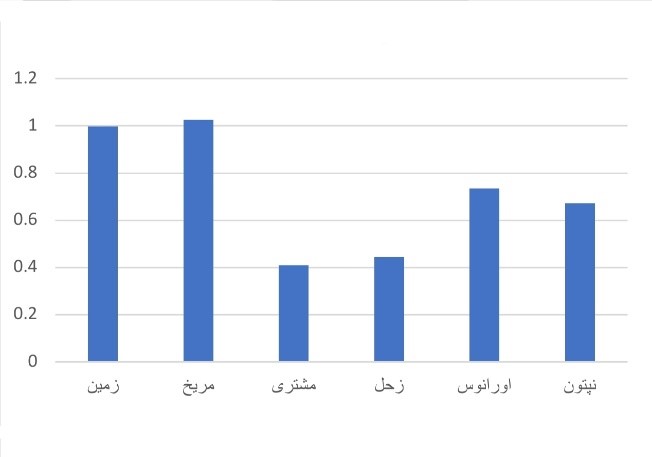
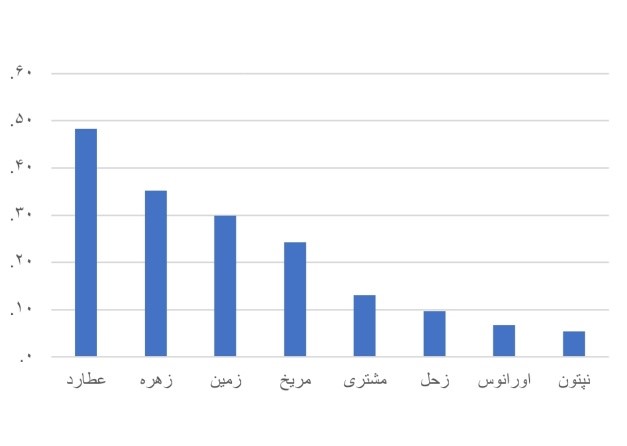
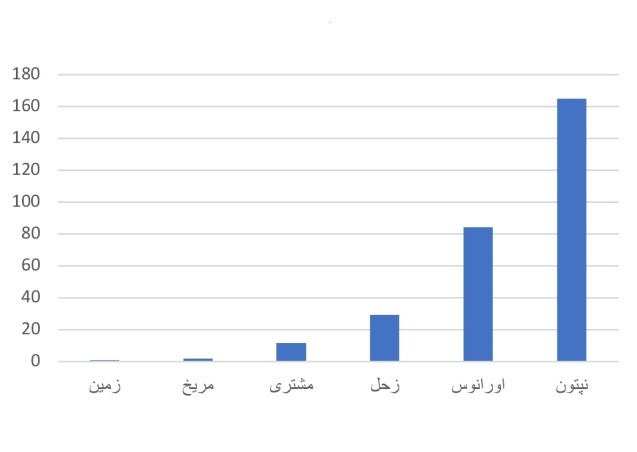
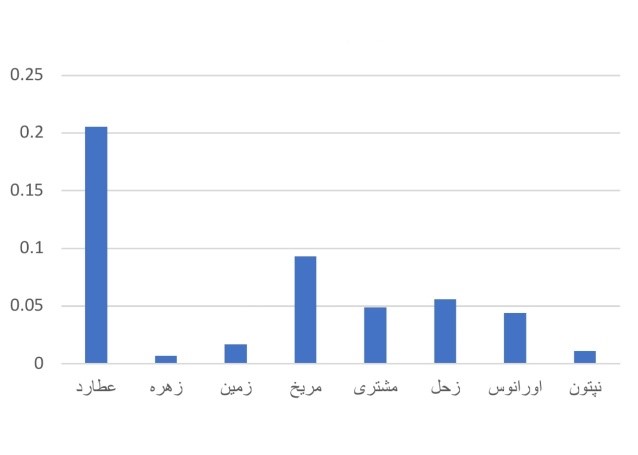
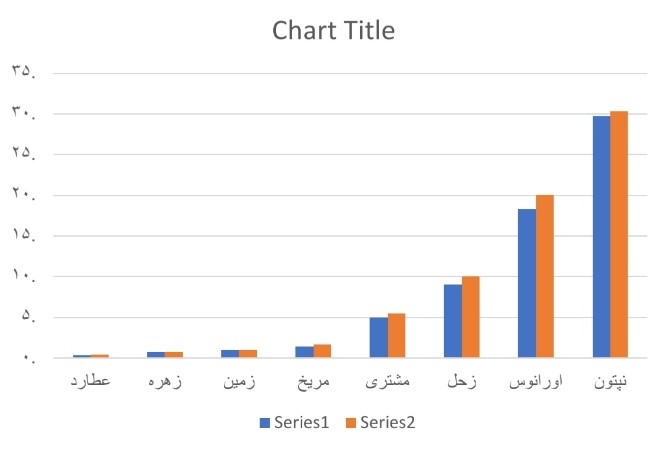
نمودارها و جدول‌ها

نکته: در نمودار ۱ به دلیل سرعت کم و در نمودار ۲ به دلیل مدت زمان زیاد و در نمودار ۴ به دلیل مدت زمان کم، نتوانستم عطارد و زهره را در نمودار بیاورم.

پایان مطلب

امیدوارم برایتان مفید واقع شده باشد.

کیارش قادری    19/5/1400 – ۲۳/۵/۱۴۰۰

▪︎ منابع:

سایت‌ها:

دیجی رو              ویکی پدیا

دانشنامه رشد       .star98tir

کتاب‌ها:

نجوم به زبان ساده  |  نویسنده: مایردگانی  |  مترجم: محمدرضا خواجه پور  |  از موسسه جغرافیایی و کاتوگرافی گیتاشناسی

زمین در فضا ( منظومه شمسی )  |  نویسنده: مهندس احمد دالکی  | از موسسه جغرافیایی و کاتوگرافی گیتاشناسی

اطلس جهان امروز  |  از موسسه گیتاشناسی نوین

نرم افزار‌ها:

Solar walk 2 free                    Solar system scope

با تشکر از آقای همایونی که مرا در بهبود این مطلب یاری نمودند.

نویسنده و محقق: کیارش قادری